Physics and Mathematics of Biological Systems

Biophysics involves applying principles, methods, and techniques from physics, such as forces, thermodynamics, and quantum mechanics, to the study of biological systems. The scope of biophysical research ranges from processes within the cell to entire ecosystems.

In this area we are interested in the nonlinear dynamics of genetic networks, and synthetic genetic oscillators with cell-to-cell communication.

We have a microfluidics laboratory in the IMS. Microfluidics is a state-of-the-art technology that offers tremendous experimental possibilities. Cells can be cultured in miniaturised culture chambers and their behaviour observed in real-time. For example, we are combining microfluidics and cell culture techniques to assess neurotoxicity in the neuromuscular system.

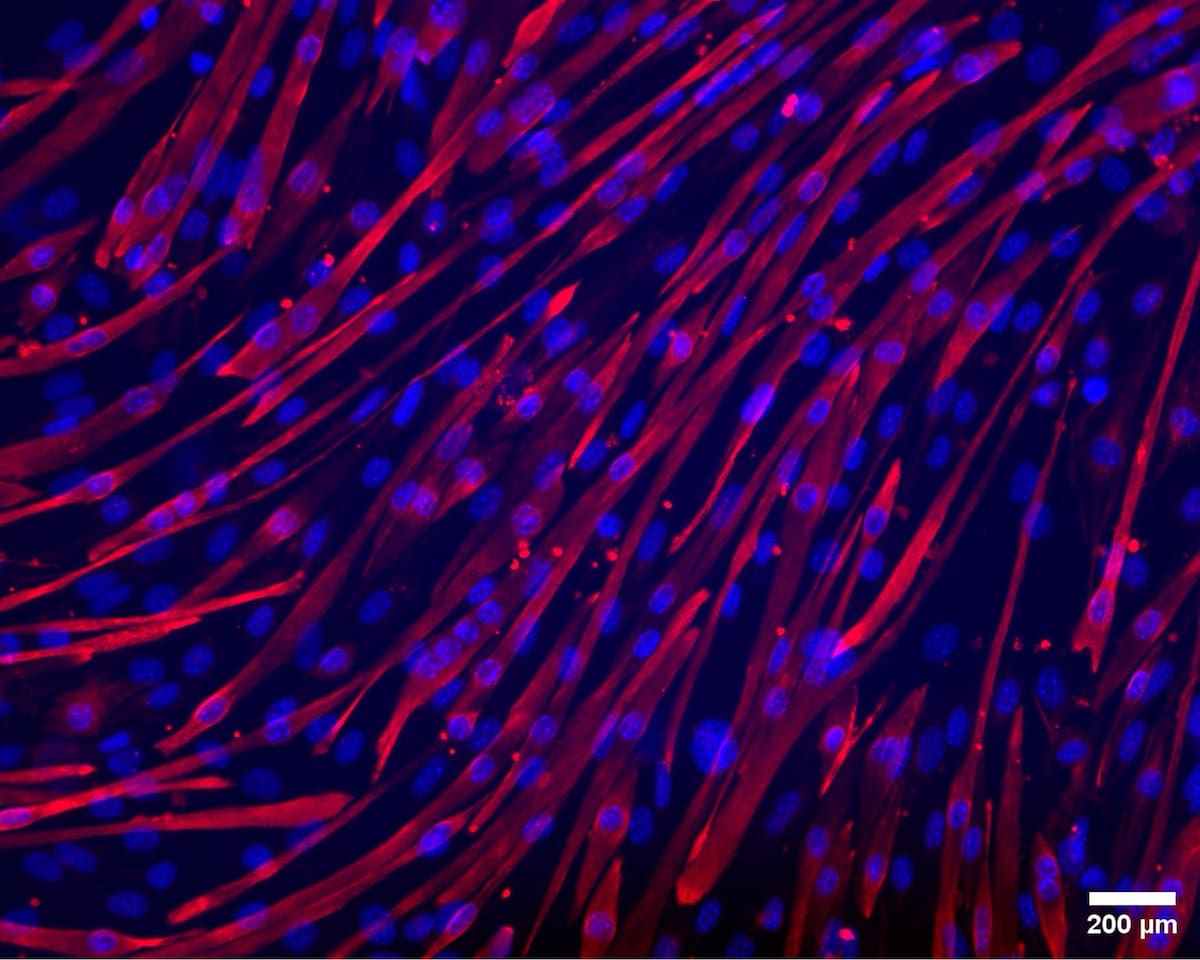
Right: Culture of mouse muscle cells (C2C12). Mature muscle fibres are stained red using Desmin and blue using Hoescht. Image: Amrita Debnath / Claudiu Giuraniuc.

Staff contacts: Ekkehard Ullner, Claudiu Giuraniuc, David McGloin.

Medical physics applies principles and methods from physics to medicine and healthcare. Particularly important are technologies developed using principles from physics to diagnose and treat disease, such as MRI, PET, ECG, imaging, and radiation therapy.

Our microfluidics laboratory designs and fabricates organ-on-chip devices for biomedical research. Our chips offer unprecedented experimental possibilities and solutions in areas such as neuroscience, myocardial infarction, cancer, and thrombosis.

We are interested in modelling patient flow and length-of-stay in hospitals using transport models and machine learning.

Using time series analysis we study aspects of critical care medicine, particularly prediction of patient deterioration and transitions to mechanical ventilation using data measured in Intensive Care Units.

We also study transitions to depressive episodes using recurrence analysis and ECG data. While transitions to depression may appear gradually over the course of several weeks, they may also occur abruptly. Predicting the latter could lead to timely interventions that prevent the episode or mitigate its effects.

We use mathematical modelling to study Alzheimer's disease and epilepsy. With a group of universities in Europe and Latin America, we are part of the EuroLAD-EEG Consortium, using EEG for dementia study and diagnosis.

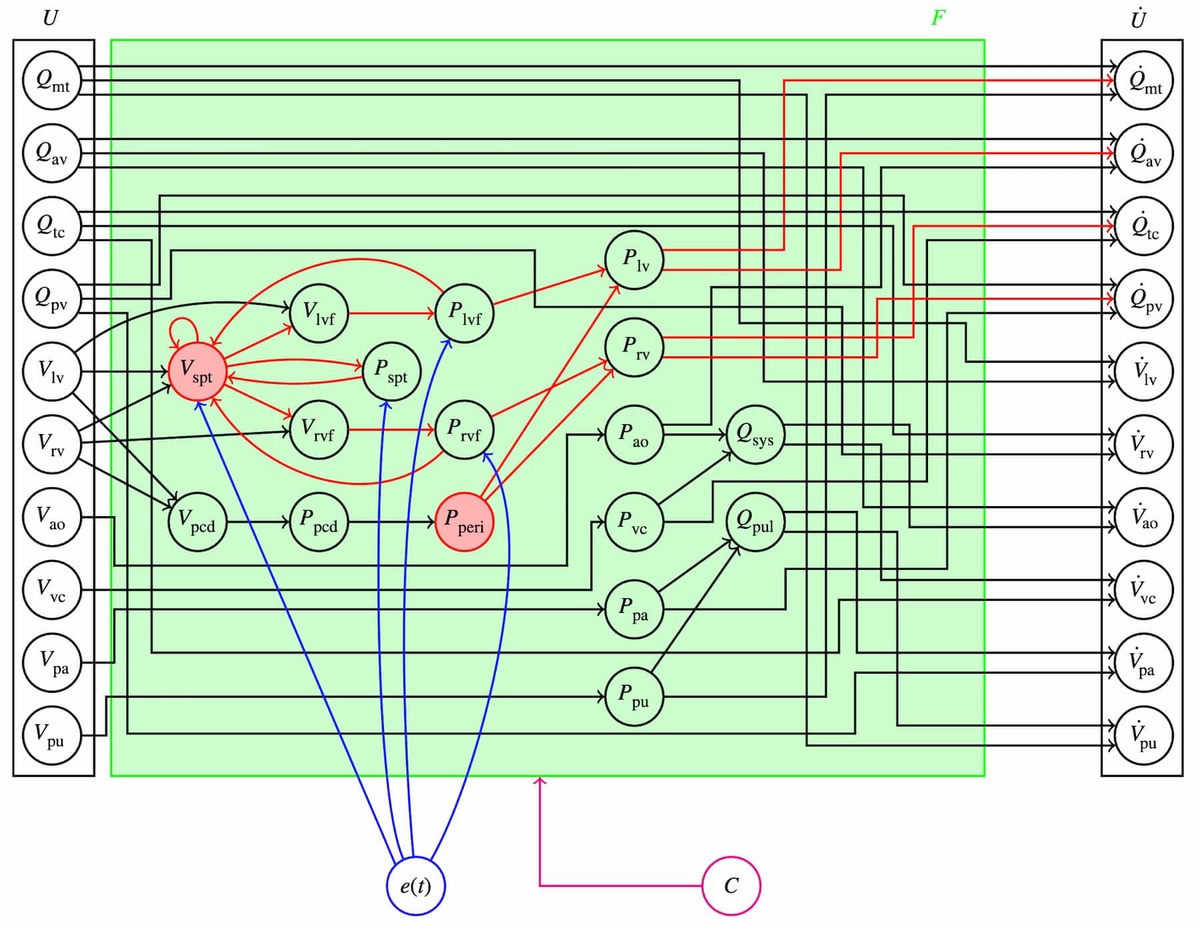
Right: Graph showing the lumped-parameter model of the cardiovascular system from Grigorian et al. (2024). The 10-dimensional state vector U on the left contains the volumes of six elastic chambers and flow rates through four valves in the heart. The graph shows how these variables contribute to the derivative of the state vector on the right.

Staff contacts: M. Carmen Romano, Murilo Baptista, Sandip George, Claudiu Giuraniuc, David McGloin, Nicolas Rubido, Marco Thiel.

In mathematical biology, we use mathematics to improve our understanding of biological systems. We develop mathematical models to understand the observed structure and behaviour of biological systems and deduce the underlying principles governing those systems.

This is a major area of research in our department. Examples of mathematical methods and principles that we use to study biological systems include (with our research areas in parentheses):

• Statistical physics (models of transport in gene expression regulation, cellular stress responses, hospital patient flow, neuronal models, DNA replication in cells, transcription, chromatin, protein and ribosome synthesis).
• Machine learning (for a list of topics, see our Data Science pages)
• Quantitative risk assessment (infectious diseases)
• Time series analysis (ecology, critical care medicine, psychiatry, depression)
• Nonlinear dynamics (for a list of topics, see our Applied Mathematics pages)
• Synchronisation (circadian rhythms, phase repulsive and inhibitory coupling)
• Topology (brain tumours)
• Statistical analysis (pathogen transmission)
• Percolation theory (infectious diseases including COVID-19)
• Stochastic modelling (DNA replication, transcription, chromatin)
• Information theory (brain network studies, ECG analysis, depression)

A major part of our work in this area is on modelling the spread and evolution of pathogens. We integrate statistical analysis, mathematical models, genomics and risk assessment to understand the transmission dynamics of bacterial gastrointestinal pathogens such as Campylobacter or Listeria. Our work on the spread of the COVID-19 pandemic was widely-publicised, and we are part of the COVID-19 Longitudinal Health and Wellbeing National Core Study. 

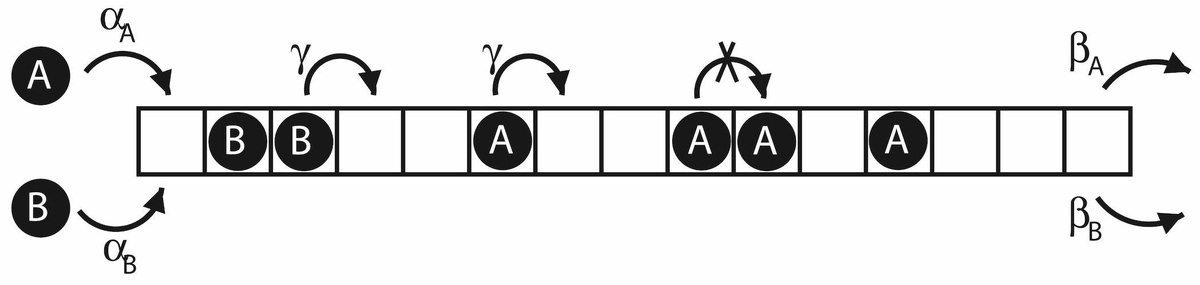
Below: Schematic showing a general transport model (TASEP) of particles along a one dimensional lattice. In Bonnin et al. (2022) we used this to model protein translation (going from mRNA to protein), where we have two different types of ribosomes (particles). This can be important to understand immune responses upon infection. A more recent application is to model patient flow in hospital. There it accounts for patients without any comorbidities and patients with multiple comorbidities, who are expected to have a slower transit rate across different wards.

Staff contacts: Francisco Pérez-Reche, Celso Grebogi, Andrew Angel, Murilo Baptista, Claudiu Giuraniuc, Alessandro Moura, M. Carmen Romano, Ekkehard Ullner, Sandip George, Nicolas Rubido.

Molecular biology seeks to understand the physical and chemical structure and behaviour of molecules that underpin the basic building blocks of life. DNA, RNA, and proteins are particularly important and widely-studied macromolecules.

We are interested in understanding fundamental biological processes using theoretical approaches based on nonlinear dynamics, statistical physics, and stochastic modelling, and comparing these models with experimental data.

In the subfield of gene expression, we study:

• RNA transcription (copying information from DNA into RNA)
• Coupling between transcription and translation (RNA to protein) using statistical physics models of transport.
• Ribosome synthesis (the molecular machines that manufacture proteins), and the relationship between ribosome synthesis and the cell cycle.
• Dynamics and regulation of protein synthesis in unicellular organisms
• Mathematical modelling of DNA replication in cells
• Chromatin
• Chaperoning of histone proteins
• Metabolic cycling in yeast

Other topics we study in this field include:

• Modelling the responses of pathogenic fungi species to combinations of stresses.
• Modelling stress responses at the cellular and molecular level.
• Bacterial homeostasis
• Macromolecular dynamics in cellular membranes

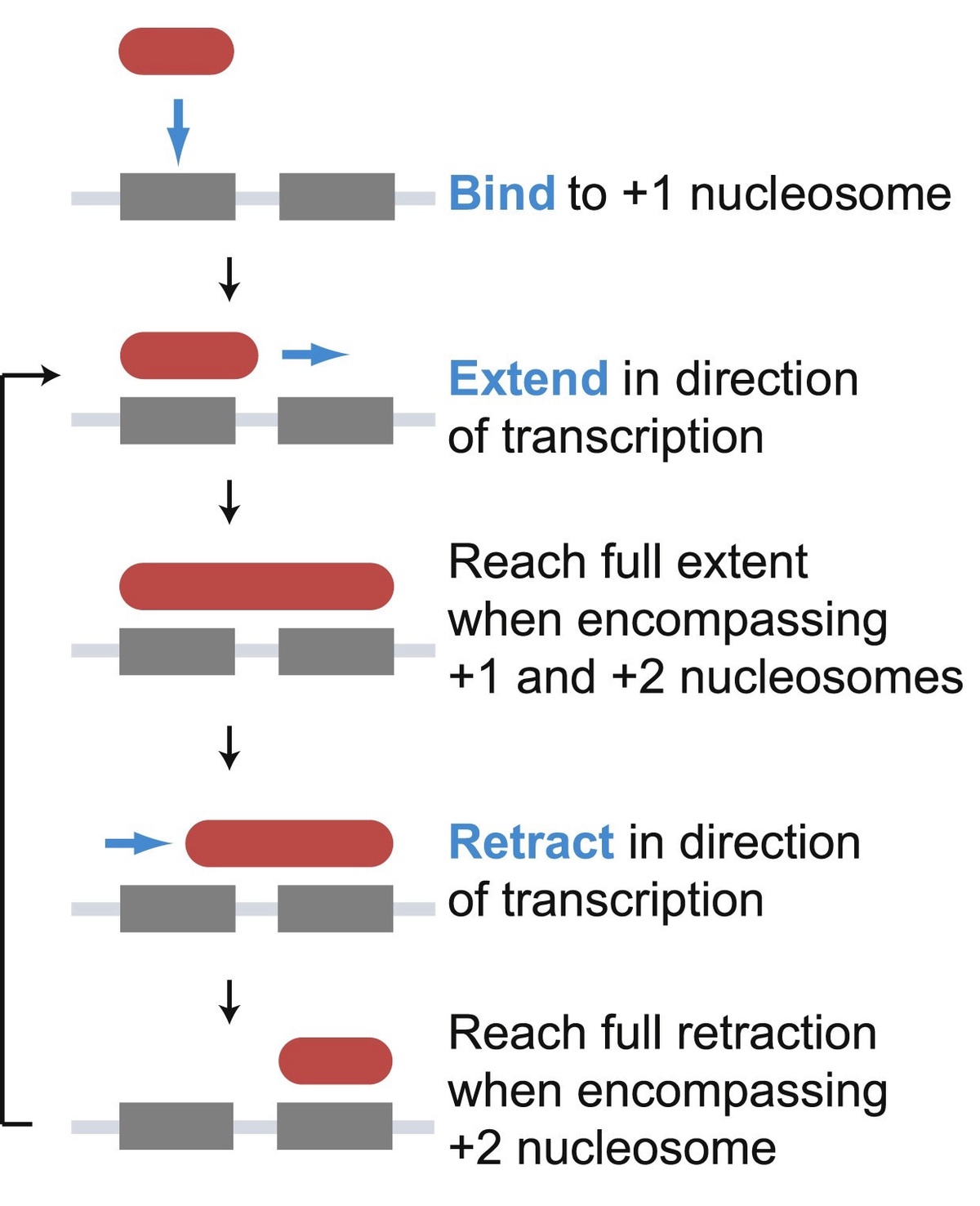
Right: Schematic showing a model of binding of the histone chaperone FACT at the +1 nucleosome and inchworm mechanism for traversing the gene. From Jeronimo et al. (2021). 

Staff contacts: Andrew Angel, Alessandro Moura, Murilo Baptista, Celso Grebogi, Francisco Pérez-Reche, Claudiu Giuraniuc, Ekkehard Ullner.

Computational neuroscience is a field where mathematical and computational techniques are used to try to understand the structure and behaviour of the nervous system, particularly the human brain, the most complex structure known to exist.

We want to understand how to infer the brain's connectivity from indirect measurements (e.g., EEGs or MRIs), and how particular pathologies (e.g., Alzheimer's disease or chronic depression) affect the brain's connectivity. Neurons in the brain create a myriad of dynamical behaviours due to their intricate connectivity and complex substrate. Our observations can only access these behaviours by indirect measurements. What data-driven conclusions can we draw from studying different states of consciousness (e.g., REM sleep)?

Our research also includes:

• Modelling synapses and their information capacity.
• Studying topological changes suffered in the brains of patients who have undergone surgery due to tumours.
• Nonlinear dynamics of biological neural networks and stochastic dynamics in neuronal models.
• Studying systems that exhibit phase repulsive and inhibitory coupling.
• Synchronisation of neuronal populations (e.g. to study epileptic seizures)

Right: Schematic from Protachevicz et al. (2024) showing (left) recovered x, active y, and inactive z neurotransmitters in a synaptic connection, and (right) their evolution over time in a periodic spike regime.

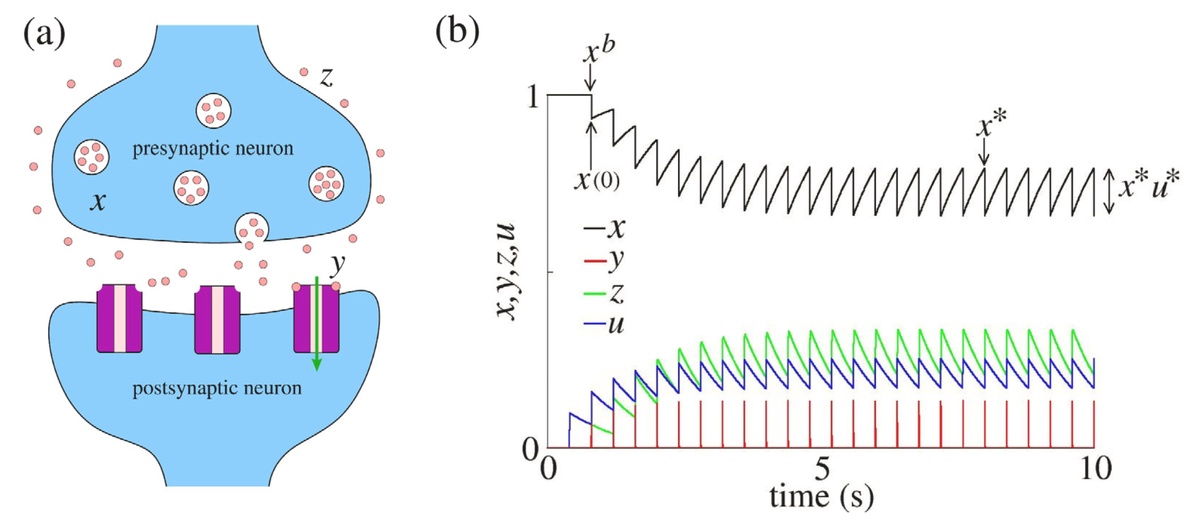
Staff contacts: Murilo Baptista, Nicolas Rubido, Ekkehard Ullner.